Economic scissors: Trial and error
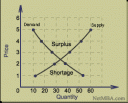
Supply and demand, the economic scissors. This beautiful diagram explains a significant amount about how economists think:
Now from what I understand, when the two curves cross we have equilibrium. This sets a price where demand and supply are equal. When the price is higher we have a surplus of goods, here some of the firms in the industry can’t sell all their produce, and so they cut prices bringing us to equilibrium. When the price is below equilibrium we have a shortage of goods. In this case competing consumers are supposed to bid up the price until we get to equilibrium.
However, in western society we don’t like to bid up the price, we just sit around. The best example I have of this is my daily pie. I want a chicken pie, I go to the store and they only ever have one, and half the time someone else has taken it. Now instead I buy a curry pie. If the store knew that I also wanted a chicken pie they could have put one more in the oven and I would have paid a higher price, and we would both be better off. Instead, they think that I have revealed a preference for curry pies and they keep on cooking them. There is imperfect information here.
How are we supposed to solve the case of the pie, given that western consumers aren’t fond of arguing up the price when there is a shortage. Well I think that firms realise this, and through a process of trial and error they try to increase information, so that they can set the equilibrium price.
The example of this is supermarkets. In a supermarket there always seems to be one type of toilet paper on special. The different manufacturers take turns, lowering there price and sometimes increasing it by more than they dropped it the next week. In this case the firms are trying to discover what the demand curve looks like, they are trying to find out if there is a shortage of their product. Through this process the firm discovers enough information bring us closer to equilibrium, all in the name of maximising profits. How convenient.

I think what’s missing from this analysis is a consideration of the transaction costs involved in information exchange. Letting people know your preferences, and them having to make a note of it, involves at least time costs to both parties. Because of this, obtaining better information is costly. It may be that the marginal payoff of obtaining better information from consumers is negative for a firm.
The transaction cost of the firm obtaining information is implicit. They would only adjust prices to gauge information if the cost of adjustment was less than or equal to the associated benifit.
I agree that there is also the possibility that the consumer could take on the transaction cost of prodiving information on their preferences. For example I could tell the people I like chicken pies, and that they should try to have another one. The reason I stuck with the firm decision approach was to show that firms choice to maximise profits could help lead to equilibrium in either direction.
The goal of the post was to introduce readers to equilibrium concepts in an accessible way, not to provide a taxonomy of equilibrium results 😉
Can you not just ask the store to stock an extra pie for you?
I could, but I’d feel like a prat, and that is a transaction cost. They make the pies in the morning you see, and then put them in the oven to warm up, they are ready by about 11am. Now if I wanted to ask for a chicken pie to be saved for me, they would have to make an extra one in the morning, keep an eye on it (to save it).
Also, I make my decision on what to eat based on my preferences at 11.30, what happens if I don’t want a pie? In this case I either buy the pie even though I don’t really want it (so that they keep on looking after one for me in the future) or I don’t go there, and they pretty much tell me to get fucked.
In a situation with all this uncertainty, the only signal that the cafe downstairs gets about my preferences comes from the pie I buy, if their chicken pies are always sold out once I get there, I will buy a curry pie, and they will assume that I like curry pies and thereby keep on making them. At one point they were making 3 curry pies and only one chicken one, however by that point not all the curry pies sold and now they have cut back to two.
Now don’t get me wrong, what you are saying Owen is another solution to the problem, I completely agree with that. However, I just want to illustrate the complications that exist getting to that damn equilibrium price.
The store is a perfect example of heartless capitalism. It cares not whether you get your chicken pie.
*picture: store owner in top hat, smoking cigar, laughing at your disappointed expression when told that there are no more chicken pies, only curry, muahahahaaa!
Hahaha, damn tophats. The people in the store are very nice, I just can’t find it within myself to give the appropriate market signal to take us to a Pareto optimal equilibrium. Damn the world!
Its only a theoretic equilibrium price anyway, and applies to an entire market rather than an individual transaction.
What I was really suggesting is not that they hold a pie for you specifically, but rather you improve the signalling information by merely asking for a chicken pie (even if you know they are out) thereby signalling to them that to have more stocks could result in more sales. Thinking about it, you are probably doing yourself a disservice by purchasing an alternative pie as it does not incent them to stock other flavours as the net result is the same to them.
Next time, ask for a chicken pie, if they dont have it, walk out and get something else. Only works if there are other choices though. Mmmmm….pie.
Indeed, Mmmmm pie.
I agree that if I signaled my interest instead of buying a substitute we could head towards equilibrium. However, it is costly for me to apply that signal, I really don’t want to go up and ask for that pie. As a result, the asymmetric information remains, and the transition to equilibrium just doesn’t happen.
The reason I am quite sure that we are out of our perfectly competitive global equilibrium is that I’ve seen other people looking for the chicken pie, and if I don’t get down there early enough (and sometimes even if i’m down there at 10.30 when the pie is still cold) the damn chicken pie is gone. I think that there is a lot more underlying demand for the chicken pies, but people like me just keep on grunting and buying the curry ones instead 😉
On a side note, I like pies because they are cheap, if I could get an equivalent lunch in some other way for only $3.90 I would be interested. If there was a chip and fish store nearby that might do the trick 😉
OK, so I can cope with being told off for talking about transaction costs. But when you then answer every other comment by citing transaction costs involved in the exchange of information??? Now I feel hard done by 😉
Hey, I said that the transaction cost was implicit. Think of it this way, you explained it in a general fashion, I just took a subset of explainations for exposition purposes. So in a sense you were more right than me 😉 . However, I thought what I wrote was sufficient for whatever point I was trying to make.
SOLUTION:
Get their phone number and call ahead to reserve the pie!
(Also works if you want to get the last blue budgie in the shop.)
So from what you have said, it is in equilibrium.
The list price of the pie does not include the transaction costs, but if you were to draw a diagram as above, you would need to include these in the ‘price’ and therefore would come to the equilibrium given the information available.
It is in a equilibrium, but not in the sense of a purely efficient market equilibrium.
If we are in a situation where the benefit to the consumer and the producer outweighs the transaction cost, but the transaction cost is greater than the benefit to the consumer or producer alone, then without some sort of co-ordination we will remain in a sub-optimal situation. This is because the consumer or producer won’t have the incentive to pay the transaction cost to get the benefit even though it is socially optimal.
In this case if one could compensate the other, or if they could share the transaction cost, then we could head towards a socially optimal equilibrium. But without that we end up in a pareto inefficient equilibrium.
But perfect competition is neither perfect nor desireable in real life. Its not a good standard to evaluate things against…
I think perfect competition is desirable, as it maximizes total surplus. All these other market imperfection simply reduce the surplus associated with the market. As it provides the maximum level of welfare, it is a useful to compare it with other situations
With all the stringent conditions that ‘perfect’ competition requires there is very little actual competition going on between firms, fine in a static environment, but in the real world which is dynamic it would result in near zero innovation – zero progress.
As long as perfect competition as a comparison is fine, as long as its not used as a reason to interfere in otherwise free markets.
Thats true, and thats an important distinction to make. Ultimately you have to decide what question you are answering.
Ultimately it depends on how much of the benefit of the given investment the firm gets. If we have a market where firms get all the benefit from their investment (it is both specific and they can extract the whole surplus that is created), then perfect competition would work fine. However, when we change those conditions there can be all sorts of complications (e.g. if your investment can be used by all other firms, then in perfect competition you only get an infinitesimal proportion of the gain, and so will hard out under-invest).
However, I’m pretty comfortable looking at the question of innovation and equilibrium adjustment separately for now, although I am sure there is plenty of interesting overlap.